How to prove the inverse of the matrix - Quora
Jordan normal form - Wikipedia
Solved 1. Calculate the inverse of the following matrices by | Chegg.com
Express the Eigenvalues of a 2 by 2 Matrix in Terms of the Trace and Determinant | Problems in Mathematics
Jordan normal form - Wikipedia
Construction of the General Solution of a System of Equations Using the Jordan Form
Formula for 2x2 inverse (video) | Khan Academy
Canonical forms of 2x2 matrices and their applications - CANONICAL FORMS OF 2 2 MATRICES AND THEIR - StuDocu
Transformation: Transfer Function ↔ State Space
Therorem 1: Under what conditions a given matrix is diagonalizable ??? Jordan Block REMARK: Not all nxn matrices are diagonalizable A similar to (close. - ppt download
PDF) Matrices of sets: -eigenvalues, eigenvectors, diagonalization -polynomials
SOLVED:Let A be the 2x2 matrix whose first row is (1, -1) and second row is (1,3). 1) Show that A has only one distinct eigenvalue: 2) Find a Jordan canonical form
Why two possibles Jordan Canonical forms of a matrix cannot be similar? - Mathematics Stack Exchange
Method of Matrix Exponential
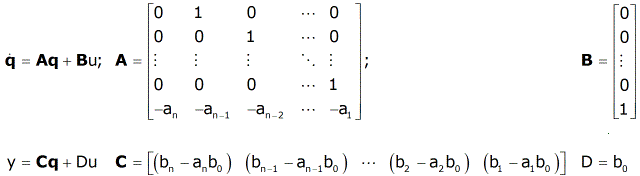
Solved 1. Consider the matrix -3 -3 (a) Find the eigenvalues | Chegg.com
Finding inverse of a matrix using Gauss - Jordan Method | Set 2 - GeeksforGeeks
Gauss Elimination Calculator - Matrix
An eigenvalue criterion for matrices transforming Stokes parameters
Chapter 6 CHAPTER SIX THE JORDAN CANONICAL FORM AND
How to understand a derivative of a matrix product (calculus, matrices, derivatives, matrix calculus, math) - Quora
What is the quickest way to find the inverse of a 4x4 or 5x5 matrix by hand? - Quora
![Solved 1) (34 pts] True or False (WRITE OUT TRUE OR FALSE, | Chegg.com](https://media.cheggcdn.com/media%2F797%2F7973512d-6f7c-4210-839f-2d52349c629c%2Fimage.png "Solved 1) (34 pts] True or False (WRITE OUT TRUE OR FALSE, | Chegg.com")
Solved 1) (34 pts] True or False (WRITE OUT TRUE OR FALSE, | Chegg.com
PDF) Square roots of 2×2 matrices
PDF) Matrix Factorial & Derivative
What are the eigenvalues and eigenvectors of the matrix [math]A= \begin{pmatrix} 0 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 0 \end{pmatrix}[/math]? - Quora
Jordan normal form - Wikipedia
